hjkl - navigation

iIaA - editing in line

xr - making change while in command mode

dd for delete line

G and gg for top and bottom lines

{,} to skip blocks of code

Using numbers to loop command

u for undo and redo

Cntrl+r for redo

yy for copying line

p for pasting line below

P for pasting line above

using dd to cut a line for pasting

use V for visual line mode to select lines

o for inserting the new line below

O for inserting new line above

d+\ to delete characters

w to jump forward words and b to jump backward

\ to jump to specific line

0 for the beginning of the line and $ for the end of the line.

^ for beginning word

W for jumping forward a word (ignore punctuation)

t+\ and f+\ to go to specific character in a line

% to go to specific block parenthesis

c+\ for changing characters

D to delete from cursor to end of line

* to search for other instances

; to go to the next instance of a character when using t,f

zz to center your page based on the cursor’s position

a to insert from the right of the character, i to insert from left

A to insert from the end of the line, I to insert from the beginning of the line

x to delete a character which cursor is on

~ to change the case of a letter

. to repeat the last executed command

r to replace a letter, R to go to replace mode

Commend combo to move a chunk of code from bottom to top

Commend combo to wrap a chunk of code

\ to search for words in the document,n goto next occurrence

Broad Phase 算法简介

​ 物理引擎通常将碰撞检测分为两(三)个阶段，Broad Phase & Narrow Phase (& Mid Phase)，其中，Broad Phase 通常使用某种Bounding Volume (Sphere,AABB,OBB,Convex Hull等)来作为物体的碰撞体来简化计算。而Narrow Phase则使用物体真实的碰撞体，进行物体是否碰撞与碰撞点的求解，将数据发送给后续的Resolve Phase。

​ 一般地，使用的Bounding Volume 越精确，False Positive 就越少。在上述列举的几种包围体中，精确度大概是凸包>OBB>AABB约等于球。

​ 本文介绍Broad Phase几种常见的算法与数据结构。重点介绍其中的SAP(Sweep And Prune)算法

Space Partioning Data Structures & Bounding Volume Hierarchy

​ 考虑这样一个情形：假设我们要对全世界所有的人进行碰撞检测，那么我们显然没有必要检测一个在北京的人与另一个在深圳的人的碰撞：这两个人离得太远了，根本不可能发生碰撞。

​ 尝试将这种思想应用进物理引擎中，就诞生了两类数据结构：空间划分树/BVH(Bounding Volume Hierarchy)树。

​ 空间划分树将空间递归地划分为若干部分，常见的空间划分数据结构有四叉树/八叉树/kDTree等。

​ BVH与空间划分树不同，它将若干包围体组成一个层次结构(Hierarchy)而非对空间进行划分。

​ 这两类数据结构实际实现起来有很多很多的细节可以讲，例如四叉树/八叉树为了适应频繁移动物体需要一些trick，BVH的构建方法等，但它们不是本文的重点。

​ Uniform Grid(均匀网格)也是一种空间划分数据结构，它将在接下来的Multi-SAP,MBP等算法出现😀

SAP Algorithm & Variants

​ 终于来到本文的重点:SAP算法。

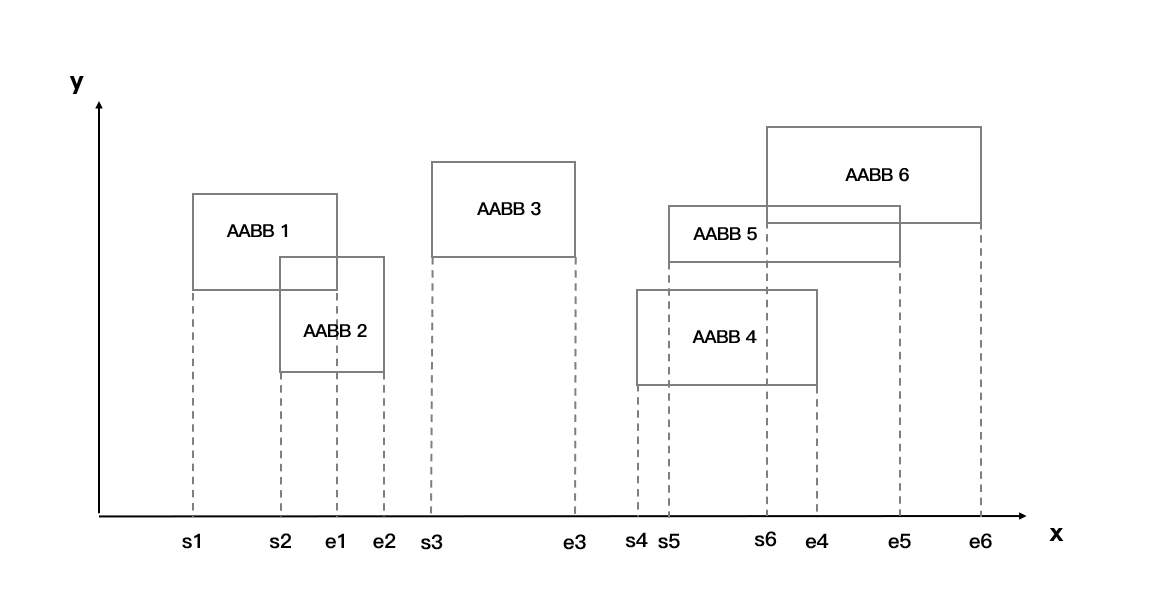
​ SAP使用最简单的包围盒之一AABB (Axis-Align Bounding Box)作为碰撞检测的对象。注意到两个AABB相交当且仅当它们在x,y,z轴上的投影都相交。因此我们可以把$n$个AABB两两相交问题转化为一轴上$n$条线段的两两相交问题。

​ 容易发现，如果直接对$n$个AABB两两碰撞检测，时间复杂度为$O(n^2)$。

Sweeping Plane Algorithm(Brute Force SAP)

​ 我们先从最简单的情况考虑。假设$n$个AABB已经被投影到某一轴上，如何判断两两相交情况？

​ 考虑ACM/OI中的差分算法：从左到右扫描，维护还未结束的线段列表。这就是Brute Force SAP的思路。

算法主要流程如下：

1. 将所有 AABB 投影至特定轴上
2. 对轴上所有区间端点进行升序排序
3. 从小到大扫描投影轴
4. 遇到一个开始端点 s(i) ，将 s(i) 所属的 AABB(i) 与 L 中的所有 s 所属的 AABB 进行相交检测, 并将 S(i) 加入至 L
5. 遇到一个结束端点 e(i) ，将与同属 e(i) 同属一个AABB 的 s(i) 从 L 中移除

Brute Force SAP的时间复杂度即为投影+扫描+排序+输出的复杂度，即在平均情况下(最劣情况很少出现，因此本文仅考虑平均情况下的时间/空间复杂度)为$O(n\log n)$。

​ 为了方便理解，这里举一个例子来说明Brute Force SAP的运行过程。

​ (source:https://github.com/phenomLi/Blog/issues/22)

TODO

SAP Description　

​ Brute Force SAP能较好地处理很多情况下的碰撞检测。但它在一些情况下还是很慢。它有几个很显著的缺点：

• 每一帧都要独立地做一次碰撞检测，没有利用好之前的信息，使得算法复杂度不优秀。
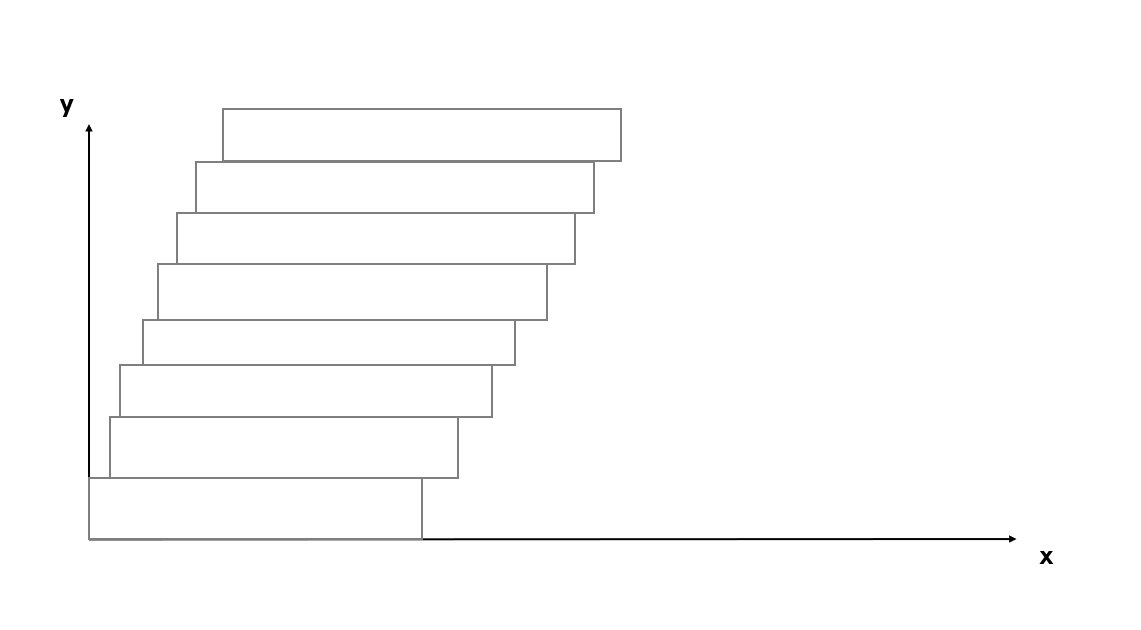
• 投影轴的选取影响性能，如下图，如果使用x轴作为投影轴，和完全的暴力算法没有明显区别。

​ 那么，如何改进呢？

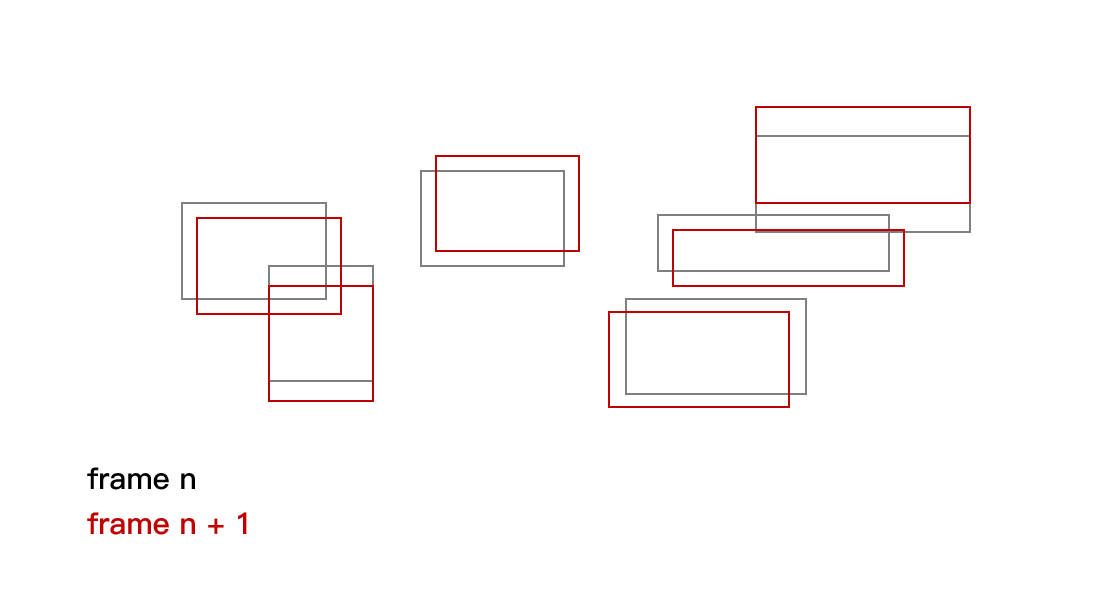
​ 考虑实际物体的物理过程，一般地，由于物体的速度相对不大，物体的位置在两帧之间不会有太大变化。

​ 我们把这种特性叫做帧相关性(frame coherence)

​ 由于帧相关性，实际排序的时候物体的位置变化不大，因此我们需要一种在序列接近有序的时候复杂度较小的排序算法，我们知道，插入排序 （Insertion Sort）在序列接近有序时的复杂度为$O(n)$，因此，我们可以选择插入排序作为我们的排序算法。

​ 由于插入排序有不同的实现方式，在本文中，插入排序特指在双重循环中，每次比较相邻两个数，如果前者较大就交换并继续比较，否则结束本层循环的算法实现。

​ 接下来，考虑Brute Force SAP的三个阶段： 投影 -> 排序 -> 扫描相交。我们能否设计一种算法能够利用好帧相关性，在上一帧存储一些信息共下一帧使用，而非帧帧独立计算，来简化这三个步骤呢？我们注意到，我们没有必要每帧都进行扫描，线段是否相交只与它们的相对位置关系有关，如果排序没有改变线段端点的相对位置，我们自然没有必要更新碰撞对的列表。我们只需要在插入排序发生交换时更新碰撞对。

​ 如下图所示：[]中的数字表示线段编号，*表示线段端点，其旁边的数字表示端点编号。u

​ 0*——[0]—*2 3*——[1]—*5

​ 1*——-[2]——-*4

​ 假设 2 号线段在移动

• 若它的1号端点(左端点)越过了 0 号线段的右端点，则 0与2停止相交
• 若它的1号端点(左端点)越过了 1 号线段的左端点，则无事发生
• 若它的3号端点(右端点)越过了 1 号线段的左端点，则 1与2开始相交
• 若它的3号端点(右端点)越过了 1 号线段的左端点，则无事发生

​ 由于运动的相对性，这四种情况能够概括所有情况。

​ 这种在排序发生交换时更新碰撞的增量式算法，就是SAP(Sweep And Prune)算法。由D. Baraff于1992年的博士论文中提出(D. Baraff. Dynamic Simulation of Non-Penetrating Rigid Bodies. PhD thesis, Cornell University, 1992)。

From 1D to 3D

​ 在Brute force SAP 中，我们只使用了一个轴作为扫描轴，并没有使用其他的轴上的信息。但在SAP中不同，我们必须更新三个轴上的信息，由于缓存友好性，通常使用再做一次单独的AABB碰撞检测的方法。（因为我们可以直接比较AABB表上的数组index，这样根本不用访问区间端点坐标，不会污染缓存）。

SAP Data Structures & Implementation Details

​ 我们讨论用何种数据结构实现SAP以及实现中的一些细节。

​ 我们使用多个数组/链表存贮AABB编号，区间信息。一般情况下，我们使用数组，因为数组形式更缓存友好(cache-friendly)。其中，每个AABB存储x,y,z坐标的引用(在x,y,z轴区间坐标的index)。对于每个区间端点，我们存储它的坐标以及是左端点还是右端点。phsyx等现代物理引擎通常使用坐标分出1bit来存贮这个信息。

​ 当向场景添加一个AABB时，我们需要做三件事：1、 分配空间 2、使线段端点插入到正确位置 3、更新碰撞对集合。一个小trick是将新添加的AABB放在充分远处(即区间数组的末尾)，再更改其坐标使之移动到正确位置。

​ 当在场景中删除一个AABB时，与更新类似，我们可以先将AABB移到充分远处，再删除之。

​ 当我们一次性在场景中添加多个物体时，我们可以考虑以下技巧(Batch Insertion)：相比于一个一个添加，我们可以先将插入物体的端点列表排好序，这样一次插入$m$个物体的时间复杂度为$O(n)$,其中$n$为现有物体数量，而非一个一个插入的$O(mn)$。

SAP Complexity Analysis

​ 在D. Baraff的原论文中，他给出了O(n+s)的复杂度时间，其中，n为AABB的数量，s为在一次排序中交换的次数。我们尝试进一步详细分析SAP的时间复杂度。

​ 考虑SAP的更新过程，我们可以分析出，SAP的时间复杂度为O(u+s+e+mn+o) 其中，u为移动AABB的数量，e为需更新AABB对的数量，s为一次排序中交换的次数，m为插入删除AABB数量，o为碰撞AABB对的总数(输出所需时间)。在物体均匀分布时可以给出$s$与$n$的关系，$s=n^{1-\frac1k}$,$k$为维度，$k=2$即2D时，时间复杂度为$O(n^{1.5})$，3D时复杂度约为$O(n^{1.66})$。

FAQ

​ （其实是我自己看论文时的一些疑问，经过思考之后想明白的）

​ -Ｑ：既然我们比较一个轴上的信息之后，直接进行一次完整的AABB检测，为什么还有维护3个轴的信息？直接维护一个轴不就行了？

​ -A：如果只保存一个轴的信息，不妨设为x轴，由于SAP是增量式算法，当物体在x轴上的投影不动，但在y轴，z轴上移动时，我们就不知道了。

Multi-SAP & Multi Box Pruning

Design Issues and Drawbacks of SAP

​ SAP算法也有一些缺点：

(a)如图所示，红色物体在y轴上移动，两个在x轴上与红色物体离得很远，静止不动，显然红色物体与蓝色物体不可能发生碰撞，但由于它们的投影在y轴上相交，当红色物体在y轴上运动时，它们的相对位置发生频繁改变，使得SAP算法频繁触发碰撞检测。这使得SAP本身的优势荡然无存。

(b) SAP插入一次物体所需的时间为O(n),即使使用批量插入方法，在AABB的数量较大时，SAP的性能仍然不优秀。

​ 一个很自然的想法是：将SAP与空间划分数据结构结合，在每个小区域内部使用SAP，

这就是Multi-SAP算法。

如上图所示：我们使用均匀网格作为空间划分数据结构。我们将空间划分为4份，在每份中单独使用SAP算法。对于那些落在边线上的点，我们将它们在出现过的区域都复制一份。

Multi-SAP可以分为三步：分配到网格中 -> 独立执行SAP -> 合并结果。如果空间划分数据结构过于复杂，会造成分配和收集的困难，得不偿失。

Multi Box Pruning

​ Multi-SAP的加速思路对Box Pruning 算法也适用。(Box Pruning 即为非增量式，只有一个投影轴的SAP)，这就是Multi Box Pruning算法。它与Multi-SAP的区别仅在于每个小空间中使用的是SAP还是Box Pruning。

​ MBP算法有优点也有缺点：

​ 优点：

• 每个小空间中物体数量很少，这使得Box Pruning执行的速度很快。
• 第二部独立执行Box Pruning的步骤可以很方便地并行化。

​ 缺点：

• 需要给定世界边界以及网格划分的参数。而额外的参数增加了调优难度。如果参数设置不好，一般效果不如SAP。
• 对于大型物体，它可能被分配到很多网格之中，这使得检测时间增加。通常，对于大型的静止物体，物理引擎会单独处理它与其它物体的碰撞，不用SAP/MBP而是使用BVH等

Broad Phase Algorithms in Physx & Unity

​ 如上图所示，Unity使用了Physx作为自己的底层物理引擎。而Physx有三种Broad Phase Algorithm，除了我们前面提到过的SAP和MBP之外，还有一种ABP(Automatic Box Pruning)。ABP在MBP的基础上，可以自动的设置世界边界以及网格参数。实践中，ABP表现相当优秀。

​ 另外，Physx的API中，对于MBP可以自己增加任意区域，但在Unity中的MBP只能设置世界边界以及世界x轴和z轴上均匀网格的数量。这就更加不推荐在Unity中使用MBP Broad Phase了。

Reference

1、Real-Time Collision Detection——Christer Ericson

2、http://www.codercorner.com/SAP.pdf

3、Efficient Large-Scale Sweep and Prune Methods with AABB Insertion and Removal Daniel J. Tracy et. al.

Mi 11 Pro 使用体验

想记录下自己使用小米11Pro若干月以来的一些想法。

购买体验

我是2021年4月2号于小米官方商城首发购买的12 + 256 GB （颜色）版本的Mi 11 Pro。购买体验良好，几乎不需要抢购，货源充足，点个赞！(当然也有可能是被Ultra抢了风头，我印象中Ultra还是需要抢购的)

外观

性能&发热

拍照

MIUI

我不是任何手机品牌的粉丝，使用过华为，小米，一加，苹果的手机，但是任何品牌都没有忠诚度可言233；对我而言，让我更换手机时再次选择同样品牌的手机的最主要的原因便是该手机系统的用户粘性。但是我还是很喜欢雷总的233。

Mi 11 Pro 是我个人购买并使用的第四部小米手机。之前使用过红米Note，红米Note3，小米5s（可以看到价格是逐渐上升的233）我印象中这几部手机的使用体验都还是不错的。根据我之前的使用体验，小米手机的最大亮点即为MIUI，功能齐全，个性化也做得很好。然而仅就我这一个月的使用体验而言，MIUI12/12.5做的远远不够。

充电&续航

总结&对小米的展望

GJK算法

Gilbert–Johnson–Keerthi 算法(GJK算法)是碰撞检测Narrow-Phase常用的一种算法。可以计算二维或者三维的碰撞。以下介绍二维情况，且可以被比较简单地推广到三维。

预备知识

闵可夫斯基差

两个集合的闵可夫斯基差(Minkowski Difference) $A\ominus B = \{x-y|x\in A\space \land\space y \in B\}$

则$A\cap B \neq \emptyset \Leftrightarrow O \in A\ominus B$

可以证明，如果$A,B$都是凸多边形，那么$A\ominus B$也是凸多边形，且$A\ominus B$的顶点的来源是$A,B$的顶点。

如此，我们可以考虑如下算法：

1
2
3
4
5
6
7
8
9
10
11

bool bruteForce(Polygon A,Polygon B)
{
    vector<Vector3> points;
	for(auto vertexa : A.vertex){
        for(auto vertexb : B.vertex){
        	points.push_back(vertexa - vertexB);
        }
    }
    Polygon minkowskiDiff = FindConvexHull(points);
    return minkowskiDiff.hasOrigin();
}

上述算法的复杂度是$O(n^2logn)$

支持向量与支持函数

对于集合$A$定义支持函数(support function)如下：

$support(A,\vec d) = \underset{a \in A}{argmax}\space \vec a \cdot\vec d $

即集合$A$中所有点中与$\vec d$点乘最大的点，也即在$\vec d$方向上最远的点，称$\vec d$为支持向量。

可以证明，若$A$是一个凸多边形，则当$\vec d$旋转一周后，$support(A,\vec d)$正好遍历每个顶点一次。

于是不难发现有$support(A\ominus B,\vec d) = support(A,\vec d)-support(B,-\vec d)$

GJK算法实现

求出整个$A\ominus B$需要$O(n^2logn)$的时间，这是我们不能接受的。于是我们考虑维护一个单纯形(即确定一块区域的最简图形，二维为三角形，三维为四面体)，如果这个三角形包含远点，则$O\in A\ominus B$。如果它不包含，我们通过求解逐步调整这个三角形使他逼近远点，直到不能继续为止(详见参考资料/ppt)。

直接上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

public class GJK : MonoBehaviour
{
    private static Vector3 findFurthest(List<Vector3> vertexs,Vector3 dir){
        //求解support(A,dir)
        Vector3 res = vertexs[0];
        float maxVal = Vector3.Dot(res,dir);
        foreach(var vertex in vertexs){//遍历所有顶点
            if(Vector3.Dot(vertex,dir) > maxVal){
                maxVal = Vector3.Dot(vertex,dir);
                res = vertex;
            }
        }
        return res;
    }
    private static Vector3 support(List<Vector3> polygonA,List<Vector3> polygonB,Vector3 dir){
    //求解support(A-B,dir)
        return findFurthest(polygonA,dir) - findFurthest(polygonB,-dir);
    }
    public static bool nextSimplex(List<Vector3> simplex,ref Vector3 d){
    //求下一个单纯形
        if(simplex.Count == 2){
            return lineCase(simplex,ref d); //两个点的情况
        }
        return triangleCase(simplex,ref d);//三角形的情况
    }
    public static bool lineCase(List<Vector3> simplex,ref Vector3 d){
        Vector3 B = simplex[0],A = simplex[1];
        Vector3 AB = B - A,AO = -A;
        //与AB垂直，指向原点的向量
        Vector3 ABp = Vector3.Cross(Vector3.Cross(AB,AO),AB);
        d = ABp;
        return false;
    }
    public static bool triangleCase(List<Vector3> simplex,ref Vector3 d){
    	//按C,B,A顺序加入单纯形的三个点
        Vector3 C = simplex[0],B = simplex[1],A = simplex[2];
        Vector3 AB = B - A,AC = C - A,AO = -A;
       	//与AB垂直的向量
        Vector3 ABp = Vector3.Cross(Vector3.Cross(AC,AB),AB);
        //与AC垂直的向量
        Vector3 ACp = Vector3.Cross(Vector3.Cross(AB,AC),AC);
        //在R_AB区域
        if(Vector3.Dot(ABp,AO) > 0){
            simplex.Remove(C);
            d = ABp;
            return false;
        }
        //在R_AC区域
        if(Vector3.Dot(ACp,AO) > 0){
            simplex.Remove(B);
            d = ACp;
            return false;
        }
        //在三角形内部
        return true;
    }
    public static bool gjk(List<Vector3> polygonA,List<Vector3> polygonB){
        Vector3 d = support(polygonA,polygonB,Vector3.right);//初始支持向量是任意方向
        List<Vector3> simplex = new List<Vector3>();
        simplex.Add(d);
        d = -d;//调整支持向量指向远点
        while(true){
            Vector3 A = support(polygonA,polygonB,d);
            if(Vector3.Dot(A,d) < 0){
                return false; //不可能包含原点
            }
            simplex.Add(A);
            if(nextSimplex(simplex,ref d)){//求下一个单纯形
                return true;
            }
        }
    }
}

参考资料

https://www.youtube.com/watch?v=MDusDn8oTSE

https://www.youtube.com/watch?v=ajv46BSqcK4

https://blog.winter.dev/2020/gjk-algorithm/

http://realtimecollisiondetection.net/pubs/SIGGRAPH04_Ericson_GJK_notes.pdf

https://zhuanlan.zhihu.com/p/113415779

Indie Camp 2019游记

​ 记我的第一次Game Jam之旅。

​ 我最早知道Game Jam这么个东西是看谜之声的视频知道的，谜叔在每期Ludum Dare结束后都会选择一些有趣的作品做成实况，其中真的有许多很棒的作品。我知道的很多独立游戏就是从某届Ludum Dare的demo完善出来的，例如Baba Is You，Mini Metro等。这一次听说有一个Game Jam可以参加，还包来回车票以及食宿，相当于免费去上海玩一圈，这种好事肯定要报名啊🤣

Day 1 2019.12.13

​ 请了一天假，周五早上从武汉出发。

Day 2 2019.12.14

Day 3 2019.12.15

感悟与总结

微积分（上）期中考试题解

​ 这次考试不算难，没有有意思的或者值得总结的题，写题解意义不大，我就是想练练$\LaTeX$而已（手动滑稽）。

T1 求数列极限$l = \lim\limits_{n \to \infty}{\sqrt[n]{2\sin^2n+3\cos^2n}}$

解：注意到${\sqrt[n]{2}\leq\sqrt[n]{2\sin^2n+3\cos^2n}} = {\sqrt[n]{2+\cos^2x}}\leq \sqrt[n]{3}$

且$\lim\limits_{n \to \infty}{\sqrt[n]{2}=\lim\limits_{n\to \infty}{\sqrt[n]{3}}=1}$

由夹挤准则 $\lim\limits_{n \to \infty}{\sqrt[n]{2\sin^2n+3\cos^2n}}=1$

T2 求无穷小$u(x)=\sqrt[3]{x^2}-1 (x\to1)$关于$x-1$的主部和阶数。

解：$\displaystyle u(x) = \left[1+(x-1)\right]^{\frac23}-1\sim\frac23(x-1)$

主部为$\frac23(x-1)$,阶数为$1$

T3 求极限$\displaystyle l =\lim\limits_{x\to0}{\frac{x\cos{x}+\sin{x}}{x\ln{\cos{x}}}}$

解：

T4计算极限$l=\lim\limits_{x\to0}(e^x-\sin x)^{\frac{1}{x^2}}$

解：

T5设$\displaystyle f(x)={x}^{\tan x}$,求$\displaystyle f’(\frac{\pi}{4})$。

解：求导得$\displaystyle f’(x)=x^{\tan x}(\sec^2 x\ln x+\frac{\tan x}{x})$

带入$\frac{\pi}{4}$得$\displaystyle f’(\frac{\pi}{4})=1+\frac\pi2\ln\frac\pi4$

T6求曲线$\cos x+\ln(y-x)=y^2$在$(0,1)$处的切线方程。

解：两边求导，带入$x=0,y=1$得到$y’(0)=-1$

故切线方程为$y=-x+1$

T7设$f(x)$二阶可导，$y=f(\sin x)$，求$y’’$

解：$y’=f’(\sin x)\cos x$

$y’’=f’’(\sin x)\cos^2x-f’(\sin x)\sin x$

T8设$y=x\ln x$求$y^{(6)}$

解：由Leibniz法则：

T9设函数

在$x=0$处连续且可导，求$a,b$的值。

解：$a=-2,b=1$，步骤略。

T10

T13证明：当$n$为奇数时，实系数多项式函数$f(x)=x^n+a_1x^{n-1}+a_2x^{n-2}+\ldots+a_n$至少有一个零点。

解：当$n$为奇数时，$\lim\limits_{x\to+\infty}f(x)=+\infty$，$\lim\limits_{x\to-\infty}f(x)=-\infty$

故$\exists x_1,x_2,s.t.f(x_1)>0,f(x_2)<0$

由介值定理$\exists x_0,f(x_0)=0$

即$f(x)$至少有一个零点。

T14设$f(x)$在$x=2$处可导，且$f(2)\not = 0$,求数列极限$\displaystyle\lim\limits_{n\to\infty}{\left[\frac{f(2+\frac1n)}{f(2)}\right]^n}$

T15求函数$f(x)=x\cos{x}$的带peano余项的5阶Maclaurin多项式。

解：$\displaystyle\cos x=1-\frac12x^2+\frac1{24}x^4+o(x^5)$

$\displaystyle x\cos x=x-\frac12x^3+\frac1{24}x^5+o(x^6)$

T16设数列$\{x_n\}$满足：$x_1=\sqrt6$,$x_{n+1}=\sqrt{6+x_n}$证明极限$\lim\limits_{n\to\infty}{x_n}$存在并求其值。

解：假设$\sqrt6 \leq x_n\leq3$,则$\sqrt6\leq x_{n+1}=\sqrt{6+x_n}\leq3$,$n=1$时,$\sqrt6\leq x_1=\sqrt6\leq3$

由数学归纳法，$\forall n \in \mathbb{N}^*$有$\sqrt6 \leq x_n\leq3$

所以$\{x_n\}$单调递增，由单调有界收敛准则$\lim\limits_{n\to\infty}{x_n}$存在，设$\alpha=\lim\limits_{n\to\infty}{x_n}$

对等式$x_{n+1}=\sqrt{6+x_n}$两边对$n\to\infty$取极限，有$\alpha=\sqrt{6+\alpha}$

即$\alpha^2-\alpha-6=0$,解得$\alpha=3$或$\alpha = -2$(舍)

因此$\lim\limits_{n\to\infty}x_n=3$

T17设$0<a<b$,$f(x)$在闭区间$[a,b]$上连续，开区间$(a,b)$上可导，证明：

解：设$\displaystyle F(x)=\frac{f(x)}{x}$,$\displaystyle g(x)=-\frac1x$,则$f(x)$,$g(x)$在闭区间$[a,b]$上连续，开区间$(a,b)$上可导,且$g’(x)\not=0$

由Cauchy中值定理

即

化简得$f’(\xi)\xi-f(\xi)=\displaystyle\frac{af(b)-bf(a)}{b-a}$即为所求。

我与这个学校的某些人格格不入。

愿中国青年都摆脱冷气，只是向上走，不必听自暴自弃者流的话。能做事的做事，能发声的发声，有一分热，发一分光，就令萤火虫一般，也可以在黑暗里发一点光，不必等候炬火。此后如竟没有炬火，我便是唯一的光。

关于此博客

​ 一直以来都有写博客的想法，但由于各种原因一直没有开始着手。2018年7月21日我建立了自己的第一个博客（现已不再使用）。本博客建立于2019年8月31日。

​

Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub.

Quick Start

Create a new post

1

$ hexo new "My New Post"

More info: Writing

Run server

1

$ hexo server

More info: Server

Generate static files

1

$ hexo generate

More info: Generating

Deploy to remote sites

1

$ hexo deploy

More info: Deployment